本文重点研究了离心泵叶轮的动态特性。

Muhammad Ashri, Saravanan Karuppanan

Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia.

摘 要：在过去的50年中，涡轮机械设计经历了快速的发展。这一领域的进步涉及多个学科的交叉，包括应力分析、振动分析、流体动力学、热力学和材料选择。其中，模态分析是开发承受动态载荷的机械零部件时常用的主要分析方法之一。本文重点研究了离心泵叶轮的动态特性，所研究的动态特性仅限于固有频率和模态振型。本研究选择的叶轮是带有径向叶片的单吸叶轮。采用有限元法（FEM）进行分析，因为这一方法已被证明是对部件或系统进行振动行为分析的实验方法的有效替代方案。叶轮的建模和仿真分别使用ANSYS Bladegen和ANSYS Workbench软件进行。在研究过程中，观察到了特征值和特征向量，分别代表了叶轮的频率和相应的模态振型。研究结果表明，叶轮叶片数量和叶片厚度的变化对频率的影响较小。然而，叶轮盘（盖板）厚度的变化对叶轮的固有频率却有显著的影响。

关键词：离心泵叶轮；模态分析；叶片数量及厚度；盖板厚度；固有频率影响

前言

叶轮是泵内的一个关键旋转零件，其功能是提升液体、气体和蒸汽的压力，从而推动流体向朝着所需方向流动。叶轮通过将电机的能量转化为流体的动能，产生离心力，加速流体的排出。叶轮通常由铁、钢、青铜、黄铜、铝或塑料等材料制成。叶轮有多种型式，如开式叶轮、半开式叶轮、闭式叶轮，以及单吸叶轮和双吸叶轮。叶轮类型的选择取决于系统压力要求和泵送流体的特性。

叶轮由一个称为轮毂的旋转盘组成，叶片则连接在轮毂上。叶轮叶片的旋转运动使流体向外流动^[1]。叶轮安装在旋转轴上，而旋转轴通常与电动机轴直联，以极高的速度旋转，从而会产生持续的振动。

离心泵是许多行业中最常见的设备，因为它简单、高效、价格便宜^[2]。叶轮对泵的性能影响很大。泵的变型通常是通过修改叶轮来设计的。叶轮经常暴露在恶劣的运行工况下，如来自吸入侧流体的冲击、叶轮本身连续旋转的振动和疲劳。这些恶劣的运行工况会影响泵的性能。因此，叶轮的动态分析对于评估泵的性能至关重要。Ziaei Rad进行了一项这样的工作^[3]，其中对不同叶片数量和盖板厚度的径向叶轮进行了模态测试和模态分析，结果表明固有频率发生了显著变化。Subramaniam^[4]对离心泵叶轮进行了模态分析，以了解叶片厚度变化引起的频率变化。本文进一步扩展了模态分析，包括叶片数量和圆盘（盖板）厚度。模态分析的范围仅限于叶轮的固有频率和振型。

叶轮叶片的有限元建模

采用有限元法（FEM）对不同参数的开式单吸叶轮进行了模态分析。FEM是一种广泛使用的振动分析方法^[3-5]。它能够分析任何任意形状的组件并得出可接受的结果。在这项研究中，选择用于叶轮模态分析的有限元工具是ANSYS Workbench软件。用于分析的叶轮的3D模型是使用ANSYS Workbench的Bladegen功能生成的^[6]。建模过程是有限元分析预处理阶段的一部分。然后将生成的叶轮模型连接到ANSYS模态分析平台，以继续进行模态分析。用于分析的基本叶轮几何形状如图1所示。根据该基本叶轮几何形状，还设计了其它几种叶轮几何形状，每种几何形状都有不同的叶片厚度、叶片数量和圆盘（盖板）厚度。表1显示了叶轮的不同几何形状。

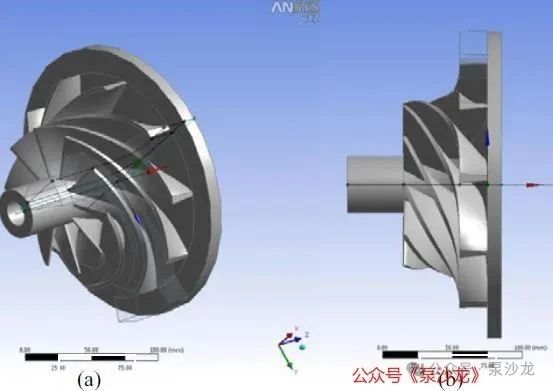
图1：基本叶轮几何形状（a）等距视图，（b）侧视图

表1：泵叶轮几何形状的变化

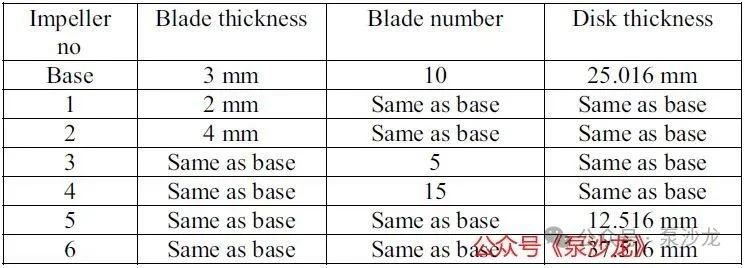
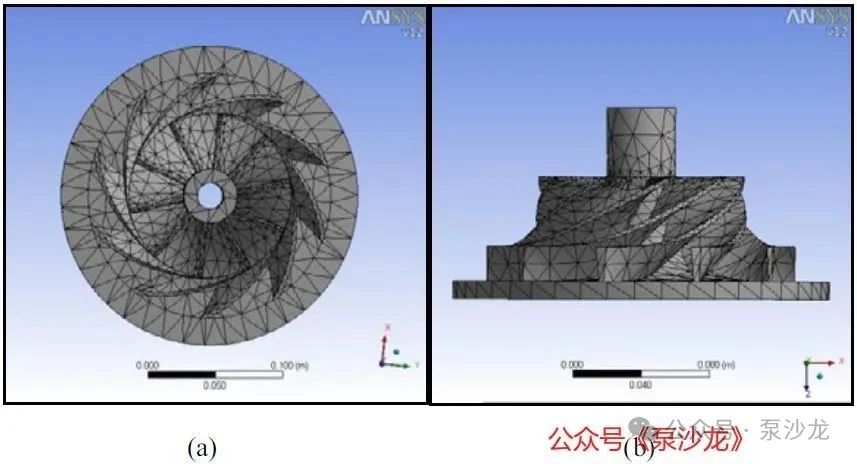
图2：基本叶轮的网格模型（a）俯视图和（b）侧视图

所考虑的材料是结构钢。材料密度为7,850 kg/m3，杨氏模量为200 GPa，泊松比为0.3，屈服强度为250 MPa，抗拉强度为460 MPa。

下一步是对模型进行适当的网格划分（离散化）。如果采用手动方式进行网格划分，可能会非常耗时且容易出错。为了解决这一问题，已经设计了大量自动生成网格的方法。在ANSYS网格划分中，用户只需选择几何体即可对网格进行设置，如曲面或边缘尺寸、网格划分方法、影响范围等。这些特征被保留在模型中，当模型设计被改变时，用户只需要“更新网格”即可获得相似的网格^[6]。基本叶轮的网格模型如图2所示。其它叶轮设计也进行了类似的网络划分。采用SOLID 185对叶轮叶片模型进行网格划分。SOLID 185^[6]是一种3D单元类型，适用于计算固有频率、变形、应力和应变，并能适当利用时间和计算机资源。

在模态分析之前，叶轮轮毂的内表面在所有自由度（DOF）上都受到约束。然后进行模型分析以确定频率和相应的振型。在该分析中，模态频率被限制为10个模态。其原因在于最低频率（对结构响应贡献最大）是主导较高频率的显著模态。

结果及讨论

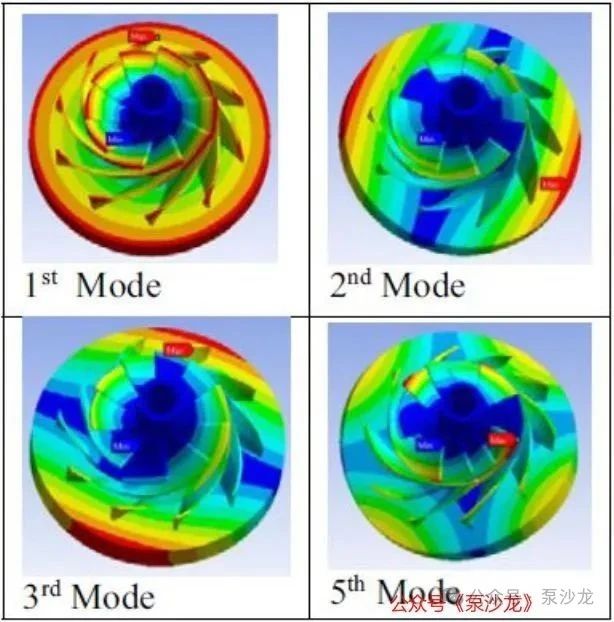
模态频率也称为固有频率，如果强迫频率与固有频率重叠时，就会产生共振现象。图3（a）显示了模态频率与叶轮叶片数量之间的关系图。从图中可以看出，随着叶片数量的变化，每个模态的频率变化非常小。这表明，叶片数量并不是影响系统固有频率的主要参数。因此，叶片数量对叶轮固有频率的影响不显著^[7]。与整个叶轮的质量和刚度相比，叶片的质量和刚度可以忽略不计。因此，叶片数量的变化对固有频率的影响也相对较小。图3（b）显示了一个基本叶轮的模态振型示例（即10个叶片，叶片厚度为0.3mm）。模态振型展示了叶轮及其叶片的弯曲模态和变形情况。观察发现，叶轮的模态振型在不同叶片数量下变化不大。对于不同叶片厚度和盘（盖板）厚度的叶轮，亦得出了类似的结论。

模态频率与叶轮叶片厚度之间的关系如图4所示。我们注意到，叶轮的模态频率呈现出轻微上升的趋势^[7]。这一发现与Subramaniam^[4]对离心泵叶轮模态分析的研究结果一致。在这两种情况下，随着叶片厚度的增加，叶轮的固有频率也随之增加。这一现象可以通过材料刚度理论来解释：当材料的质量增加时，其刚度也随之增加，固有频率的提高可能是由结构刚度的增加所引起的。

模态频率与叶轮盘（盖板）厚度之间的关系如图5所示。在第一固有模态下，每个圆盘（盖板）的频率差异较小，然而，在第2、第3和第5固有模态下，这种差异变得更加明显。对于更高的固有模态， 3个叶轮的频率差异则显著减小，变得不那么明显。图5清晰地展示了这一点，相较于较低的固有频率模态，第10个固有频率模态的频率变化较小。每个叶轮之间的频率差异是由于叶轮的质量增加造成的。当叶轮的圆盘（盖板）厚度增加时，质量随之增加，从而提升了系统的刚度加。因此，可以推断，叶轮盘（盖板）厚度是影响叶轮固有频率的关键参数。

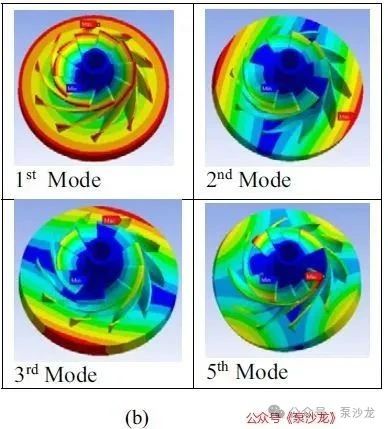
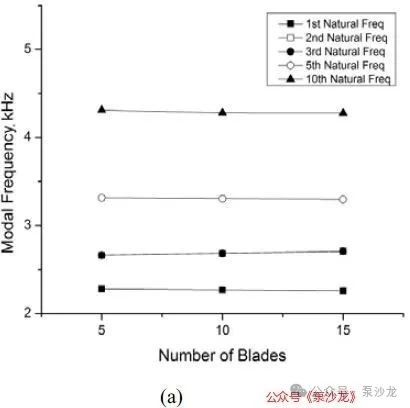
图3：基本叶轮（a）频率与叶片数量的关系，（b）t=0.3mm的10个叶轮叶片示例（样本）的模态形状

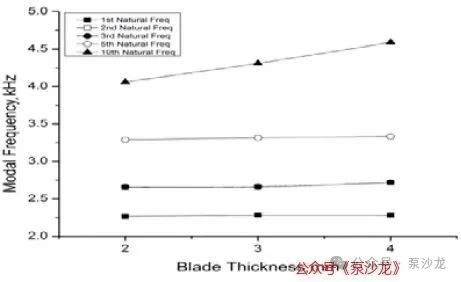
图4：频率与叶片厚度之间的关系

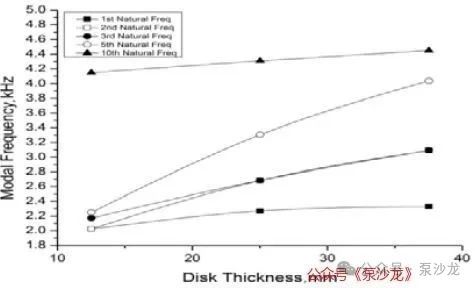
图5：频率与盖板厚度之间的关系

结论

通过有限元分析，我们对多参数叶轮进行了模态分析，提取了不同模态下叶轮的固有频率和振型。以下模态分析得出的主要结论：

1）在分析不同叶片数的叶轮时，每个叶轮的模态频率差异较小。

2）随着叶片厚度的增加，叶轮的固有频率略有上升，这一现象可归因于结构刚度的增加。

3）叶轮盖板厚度是影响其固有频率的一个主要参数，频率会随着盖板厚度的增加而增加。

参考文献

1）A.T. Oyelami, S.B. Adejuyigbe, M.A. Waheed, A.K. Ogunkoya, D. Iliya, The Pacific Journal of Science and Technology. 13(1), 24-33 (2012)

2）C. Jacobsen, The Centrifugal Pump. 5th Edition, John Wiley & Sons, 128 (2010)

3）R. S. Ziaei, Iranian Journal of Science & Technology, Transaction B – Engineering. 29(B2), 157-169 (2005)

4）L. Subramaniam, European Journal of Scientific Research. 79(1), 5-14 (2012)

5）S. Patil, S. F. Patil, and S. Karuppanan, International Journal of Applied Engineering Research, 8(14), 1685-1694 (2013)

6）ANSYS Release 12.0, Structural Analysis Guide, SAS IP, Inc. (2009)

7）Muhammad Ashri, Modal Analysis of Pump Impeller Using Finite Element Method. Final Year Project, Mechanical Engineering Department, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, Perak (2013)